
Introducing Hugging Face's new library for diffusion models
Diffusion models proved themselves very effective in artificial synthesis, even beating GANs for images. Because of that, they gained traction in the machine learning community and play an important role for systems like DALL-E 2 or Imagen to generate photorealistic images when prompted on text.
While the most prolific successes of diffusion models have been in the computer vision community, these models have also achieved remarkable results in other domains, such as:
However, most of the recent research on diffusion models, e.g. DALL-E 2 and Imagen, is unfortunately not accessible to the broader machine learning community and typically remains behind closed doors.
Here comes the diffusers library with the goals to:
gather recent diffusion models from independent repositories in a single and long-term maintained project that is built by and for the community,
reproduce high impact machine learning systems such as DALLE and Imagen in a manner that is accessible for the public, and
create an easy to use API that enables one to train their own models or re-use checkpoints from other repositories for inference.
This notebook will walk you through the most important features of diffusers.
We assume that the reader has a minimal understanding of how diffusion models function. To refresh some theory as well as terminology, we recommend reading/skimming the following blog posts:
Lilian Weng's, OpenAI, introductory post
Yang Song's, Stanford, introductory post
The Annotated Diffusion Model post
Or papers:
The original paper proposing thermodynamics for unsupervised learning,
The paper for a popular diffusion model, Denoising Diffusion Probabilistic Models DDPM, or
A recent paper covering tradeoffs in diffusion models
Summary
This post is designed to showcase the core API of diffusers, which is divided into three components:
Pipelines: high-level classes designed to rapidly generate samples from popular trained diffusion models in a user-friendly fashion.
Models: popular architectures for training new diffusion models, e.g. UNet.
Schedulers: various techniques for generating images from noise during inference as well as to generate noisy images for training.
Note: This notebook focus only on inference. If you want to get a more hands-on guide on training diffusion models, please have a look at the Training with Diffusers notebook.
Install diffusers
Looking in indexes: https://pypi.org/simple, https://us-python.pkg.dev/colab-wheels/public/simple/
Collecting diffusers==0.11.1
Downloading diffusers-0.11.1-py3-none-any.whl (153 kB)
|████████████████████████████████| 153 kB 16.0 MB/s
Requirement already satisfied: filelock in /usr/local/lib/python3.7/dist-packages (from diffusers==0.11.1) (3.8.0)
Requirement already satisfied: numpy in /usr/local/lib/python3.7/dist-packages (from diffusers==0.11.1) (1.21.6)
Collecting huggingface-hub>=0.8.1
Downloading huggingface_hub-0.9.1-py3-none-any.whl (120 kB)
|████████████████████████████████| 120 kB 64.2 MB/s
Requirement already satisfied: importlib-metadata in /usr/local/lib/python3.7/dist-packages (from diffusers==0.11.1) (4.12.0)
Requirement already satisfied: torch>=1.4 in /usr/local/lib/python3.7/dist-packages (from diffusers==0.11.1) (1.12.1+cu113)
Requirement already satisfied: Pillow in /usr/local/lib/python3.7/dist-packages (from diffusers==0.11.1) (7.1.2)
Requirement already satisfied: regex!=2019.12.17 in /usr/local/lib/python3.7/dist-packages (from diffusers==0.11.1) (2022.6.2)
Requirement already satisfied: requests in /usr/local/lib/python3.7/dist-packages (from diffusers==0.11.1) (2.23.0)
Requirement already satisfied: tqdm in /usr/local/lib/python3.7/dist-packages (from huggingface-hub>=0.8.1->diffusers==0.11.1) (4.64.0)
Requirement already satisfied: packaging>=20.9 in /usr/local/lib/python3.7/dist-packages (from huggingface-hub>=0.8.1->diffusers==0.11.1) (21.3)
Requirement already satisfied: typing-extensions>=3.7.4.3 in /usr/local/lib/python3.7/dist-packages (from huggingface-hub>=0.8.1->diffusers==0.11.1) (4.1.1)
Requirement already satisfied: pyyaml>=5.1 in /usr/local/lib/python3.7/dist-packages (from huggingface-hub>=0.8.1->diffusers==0.11.1) (6.0)
Requirement already satisfied: pyparsing!=3.0.5,>=2.0.2 in /usr/local/lib/python3.7/dist-packages (from packaging>=20.9->huggingface-hub>=0.8.1->diffusers==0.11.1) (3.0.9)
Requirement already satisfied: zipp>=0.5 in /usr/local/lib/python3.7/dist-packages (from importlib-metadata->diffusers==0.11.1) (3.8.1)
Requirement already satisfied: urllib3!=1.25.0,!=1.25.1,<1.26,>=1.21.1 in /usr/local/lib/python3.7/dist-packages (from requests->diffusers==0.11.1) (1.24.3)
Requirement already satisfied: idna<3,>=2.5 in /usr/local/lib/python3.7/dist-packages (from requests->diffusers==0.11.1) (2.10)
Requirement already satisfied: certifi>=2017.4.17 in /usr/local/lib/python3.7/dist-packages (from requests->diffusers==0.11.1) (2022.6.15)
Requirement already satisfied: chardet<4,>=3.0.2 in /usr/local/lib/python3.7/dist-packages (from requests->diffusers==0.11.1) (3.0.4)
Installing collected packages: huggingface-hub, diffusers
Successfully installed diffusers-0.11.1 huggingface-hub-0.9.1
Overview
One goal of the diffusers library is to make diffusion models accessible to a wide range of deep learning practitioners. With this in mind, we aimed at building a library that is easy to use, intuitive to understand, and easy to contribute to.
As a quick recap, diffusion models are machine learning systems that are trained to denoise random gaussian noise step by step, to get to a sample of interest, such as an image.
The underlying model, often a neural network, is trained to predict a way to slightly denoise the image in each step. After certain number of steps, a sample is obtained.
The process is illustrated by the following design: 
The architecture of the neural network, referred to as model, commonly follows the UNet architecture as proposed in this paper and improved upon in the Pixel++ paper.
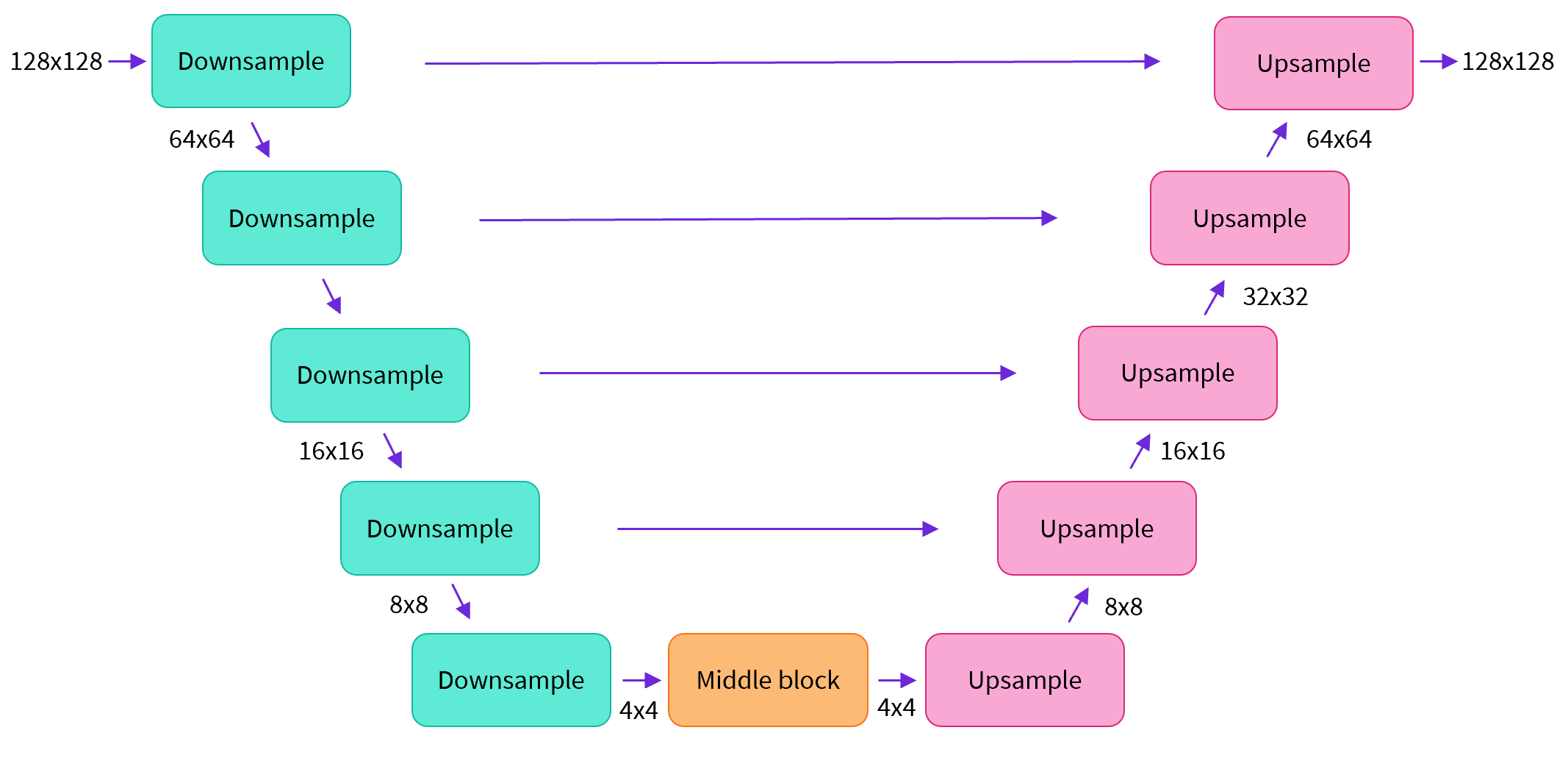
No worries if you don't understand everything. Some of the highlights of the architecture are:
this model predicts images of the same size as the input
the model makes the input image go through several blocks of ResNet layers which halves the image size by 2
then through the same number of blocks that upsample it again.
skip connections link features on the downsample path to corresponding layers in the upsample path.
The diffusion process consists in taking random noise of the size of the desired output and pass it through the model several times. The process ends after a given number of steps, and the output image should represent a sample according to the training data distribution of the model, for instance an image of a butterfly.
During training we show many samples of a given distribution, such as images of butterfly. After training, the model will be able to process random noise to generate similar butterfly images.
Without going in too much detail, the model is usually not trained to directly predict a slightly less noisy image, but rather to predict the "noise residual" which is the difference between a less noisy image and the input image (for a diffusion model called "DDPM") or, similarly, the gradient between the two time steps (like the diffusion model called "Score VE").
To do the denoising process, a specific noise scheduling algorithm is thus necessary and "wrap" the model to define how many diffusion steps are needed for inference as well as how to compute a less noisy image from the model's output. Here is where the different schedulers of the diffusers library come into play.
Finally, a pipeline groups together a model and a scheduler and make it easy for an end-user to run a full denoising loop process. We'll start with the pipelines and dive deeper into its implementation before taking a closer look at models and schedulers.
Core API
Pipelines
Let's begin by importing a pipeline. We'll use the google/ddpm-celebahq-256 model, built in collaboration by Google and U.C.Berkeley. It's a model following the Denoising Diffusion Probabilistic Models (DDPM) algorithm trained on a dataset of celebrities images.
We can import the DDPMPipeline, which will allow you to do inference with a couple of lines of code:
The from_pretrained() method allows downloading the model and its configuration from the Hugging Face Hub, a repository of over 60,000 models shared by the community.
To generate an image, we simply run the pipeline and don't even need to give it any input, it will generate a random initial noise sample and then iterate the diffusion process.
The pipeline returns as output a dictionary with a generated sample of interest. This will typically take 2-3 minutes on Google Colab:
Let's take a look 🙂
Looks pretty good!
Now, let's try to understand a bit better what was going on under the hood. Let's see what the pipeline is made of:
We can see inside the pipeline a scheduler and a UNet model. Let's have a closer look at them and what this pipeline just did behind the scenes.
Models
Instances of the model class are neural networks that take a noisy sample as well as a timestep as inputs to predict a less noisy output sample. Let's load a pre-trained model and play around with it to understand the model API!
We'll load a simple unconditional image generation model of type UNet2DModel which was released with the DDPM Paper and for instance take a look at another checkpoint trained on church images: google/ddpm-church-256.
Similarly to what we've seen for the pipeline class, we can load the model configuration and weights with one line, using the from_pretrained() method that you may be familiar with if you've played with the transformers library:
The from_pretrained() method caches the model weights locally, so if you execute the cell above a second time, it will go much faster. The model is a pure PyTorch torch.nn.Module class which you can see when printing out model.
Now let's take a look at the model's configuration. The configuration can be accessed via the config attribute and shows all the necessary parameters to define the model architecture (and only those).
As you can see, the model config is a frozen dictionary. This is to enforce that the configuration will only be used to define the model architecture at instantiation time and not for any attributes that can be changed during inference.
A couple of important config parameters are:
sample_size: defines theheightandwidthdimension of the input sample.in_channels: defines the number of input channels of the input sample.down_block_typesandup_block_types: define the type of down- and upsampling blocks that are used to create the UNet architecture as was seen in the figure at the beginning of this notebook.block_out_channels: defines the number of output channels of the downsampling blocks, also used in reversed order for the number of input channels of the upsampling blocks.layers_per_block: defines how many ResNet blocks are present in each UNet block.
Knowing how a UNet config looks like, you can quickly try to instantiate the exact same model architecture with random weights. To do so, let's pass the config as an unpacked dict to the UNet2DModel class.
Cool, the above created a randomly initialized model with the same config as the previous one.
If you want to save the model you just created, you can use the save_pretrained() method, which saves both the model weights as well as the model config in the provided folder.
Let's take a look at what files were saved in my_model.
diffusion_pytorch_model.bin is a binary PyTorch file that stores the model weights and config.json stores the model's configuration.
If you want to reuse the model, you can simply use the from_pretrained() method again, as it loads local checkpoints as well as those present on the Hub.
Coming back to the actually trained model, let's now see how you can use the model for inference. First, you need a random gaussian sample in the shape of an image (batch_size in_channels sample_size sample_size). We have a batch axis because a model can receive multiple random noises, a channel axis because each one consists of multiple channels (such as red-green-blue), and finally sample_size corresponds to the height and width.
Time to do the inference!
You can pass the noisy sample alongside a timestep through the model. The timestep is important to cue the model with "how noisy" the input image is (more noisy in the beginning of the process, less noisy at the end), so the model knows if it's closer to the start or the end of the diffusion process.
As explained in the introduction, the model predicts either the slightly less noisy image, the difference between the slightly less noisy image and the input image or even something else. It is important to carefully read through the model card to know what the model has been trained on. In this case, the model predicts the noise residual (difference between the slightly less noisy image and the input image).
The predicted noisy_residual has the exact same shape as the input and we use it to compute a slightly less noised image. Let's confirm the output shapes match:
Great.
Now to summarize, models, such as UNet2DModel (PyTorch modules) are parameterized neural networks trained to predict a slightly less noisy image or residual. They are defined by their .config and can be loaded from the Hub as well as saved and loaded locally. The next step is learning how to combine this model with the correct scheduler to be able to actually generate images.
Schedulers
Schedulers are algorithms wrapped into a Python class. They define the noise schedule which is used to add noise to the model during training, and also define the algorithm to compute the slightly less noisy sample given the model output (here noisy_residual). This notebook focuses only on how to use scheduler classes for inference. You can check out this notebook to see how to use schedulers for training.
It is important to stress here that while models have trainable weights, schedulers are usually parameter-free (in the sense they have no trainable weights) and simply define the algorithm to compute the slightly less noisy sample. Schedulers thus don't inherit from torch.nn.Module, but like models they are instantiated by a configuration.
To download a scheduler config from the Hub, you can make use of the from_config() method to load a configuration and instantiate a scheduler.
Let's use DDPMScheduler, the denoising algorithm proposed in the DDPM Paper.
Let's also take a look at the config here.
Different schedulers are usually defined by different parameters. To better understand what the parameters are used for exactly, the reader is advised to directly look into the respective scheduler files under src/diffusers/schedulers/, such as the src/diffusers/schedulers/scheduling_ddpm.py file. Here are the most important ones:
num_train_timestepsdefines the length of the denoising process, e.g. how many timesteps are need to process random gaussian noise to a data sample.beta_scheduledefine the type of noise schedule that shall be used for inference and trainingbeta_startandbeta_enddefine the smallest noise value and highest noise value of the schedule.
Like the models, schedulers can be saved and loaded with save_config() and from_config().
All schedulers provide one or multiple step() methods that can be used to compute the slightly less noisy image. The step() method may vary from one scheduler to another, but normally expects at least the model output, the timestep and the current noisy_sample.
Note that the step() method is somewhat of a black box function that "just works". If you are keen to better understand how exactly the previous noisy sample is computed as defined in the original paper of the scheduler, you should take a look at the actual code, e.g. click here for DDPM, which contains comments and references to the original paper.
Let's give it a try using the model output from the previous section.
You can see that the computed sample has the exact same shape as the model input, meaning that you are ready to pass it to the model again in a next step.
Let's now bring it all together and actually define the denoising loop. This loop prints out the (less and less) noisy samples along the way for better visualization in the denoising loop. Let's define a display function that takes care of post-processing the denoised image, convert it to a PIL.Image and displays it.
Before defining the loop, let's move the input and model to the GPU to speed up the denoising process a bit.
Time to finally define the denoising loop! It is rather straight-forward for DDPM.
Predict the residual of the less noisy sample with the model.
Compute the less noisy sample with the scheduler.
Additionally, at every 50th step this will display the progress.
It's important to note here that you loop over scheduler.timesteps which is a tensor defining the sequence of timesteps over which to iterate during the denoising process. Usually, the denoising process goes in decreasing order of timesteps, so from the total number of timesteps (here 1000) to 0.
Depending on your GPU this might take up to a minute - enough time to reflect on everything you learned so far while you can watch a church being built from nothing but noise ⛪.
100%|██████████| 1000/1000 [00:49<00:00, 20.37it/s]
You can see that it takes quite some time to see a somewhat meaningful shape - only after ca. 800 steps.
While the quality of the image is actually quite good - you might want to speed up the image generation.
To do so, you can try replacing the DDPM scheduler with the DDIM scheduler which keep high generation quality at significantly sped-up generation time.
Exchanging schedulers: one of the exciting prospects of a diffusion model library is that different scheduling protocols can work with different models, but there is not a one-sized fits all solution! In this case, DDIM worked as an swap for DDPM, but this not universal (and represents an interesting research problem).
The DDPM and DDIM scheduler more or less share the same configuration, so you can load a DDIM scheduler from a DDPM scheduler.
The DDIM scheduler allows the user to define how many denoising steps should be run at inference via the set_timesteps method. The DDPM scheduler runs by default 1000 denoising steps. Let's significantly reduce this number to just 50 inference steps for DDIM.
And you can run the same loop as before - only that you are now making use of the much faster DDIM scheduler.
100%|██████████| 50/50 [00:02<00:00, 20.81it/s]
You can see that the image generation is indeed much faster - a mere two seconds - but also that you pay by giving away image quality in exchange for speed.
Cool, now you should have gotten a good first understanding of the schedulers. The important things to remember are:
schedulers are parameter-free (no trainable weights)
schedulers define the algorithm computing the slightly less noisy sample during inference
They are many schedulers already added to diffusers and diffusers will be adding even more in the future. It's important that you read the model cards to understand which model checkpoints can be used with which schedulers. You can find all available schedulers here.
To end the chapter about models and schedulers, please also note that we very much deliberately try to keep models and schedulers as independent from each other as possible. This means a scheduler should never accept a model as an input and vice-versa. The model predict the noise residual or slightly less noisy image with its trained weights, while the scheduler computes the previous sample given the model's output.