Math 157: Intro to Mathematical Software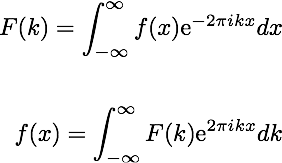
UC San Diego, Winter 2018
March 15, 2018 : Fast Fourier Transforms
Nancy Juarez-Fuertes
"4-E-AY"
Collaborators: Anastasia Guiano, Megan Chang
This Worksheet:
Overview
Real Life Applications
Common Functions
Examples
Exercises

Fast Fourier Transforms(FFT): Overview
What is FFT?
FFT is a discrete Fourier transform algorithm that samples a signal over a period of time and divides it into its frequency components.
Fourier analysis converts a dignal from its orginal domain into a frequency domain representation. FFT rapidly computes the transformation by factoring the descrete Fourier matrix into a product of sparse factors.
Were first discussed by cooley and Tukey in 1965
Gauss had already discussed the critical factorization step as early as 1805
Finding the Recipe!
Watch this video
Here's a great website that breaks down what the Fourier transform is and how it is used!
A Fourier Series is the summation of sine waves. A Fourier series can be used to represent any periodic signal.
Given a complex wave, a combination of many sine waves, (A Fourier Series), we can preform a Fourier Trandform to find the ingredients, used to create such a complex wave
We take the signal which shows us the power over a period of time, and we are transforming it into individual components which shows us the power of each wavelength, or frequency.
The Fourier Transform is a set of complicated equations.
The foureir Transform further proves how the Fourier series is a good approximation of a naturally occuring signal.
Real Life Applications
Where is the Fourier Transform used in the real world?
sound wave analysis
image data analysis
digital image processing
computer -assisted image processing
Edge detection (when you take a picture and you want to outline a person or something and transfer it to another image)
Make sure your kernel is set to "Python 3 (Ubuntu Linux)" before proceeding.
Functions used for FFT in Python:
see scipy.fftpack
One dimensional discrete Fourier Transform
Here is an example of fft and ifft
fftfreq returns sample frequency points.
Here we plot the fast fourier transform of the sum of two sine waves.
Two dimensional Fourier Transform
2-D Fourier Transforms are used in image processing. They are used to see peaks of spacial frequencies of repeated texture in images such as finger prints!
Digital Image Processing: Making an image blurry using FFT
Here is a "clear" example on how 2-D FFT applictions are applied to images.
Padded fourier transform, with the same shape as the image We use :func:scipy.signal.fftpack.fft2 to have a 2D FFT
Think about a mechanic who takes a sound sample of an engine and then relies on a machine to analyze that sample, looking for potential engine problems. The diagnostic can find some problems and visual inspection can find others, but sometimes the sound of an engine reveals issues that you can’t find in any other way.
What does this do? What are the blue lines at the bottom?
This code reads a .wav file and solves the Fourier transform! The output displays the strongest detected frequencies over time. The blue lines at the bottom are the extra noise of the signal.
Note: I found that testing this with .wav files larger than 24 kb caused a bit of trouble when reading the file.